Abstract

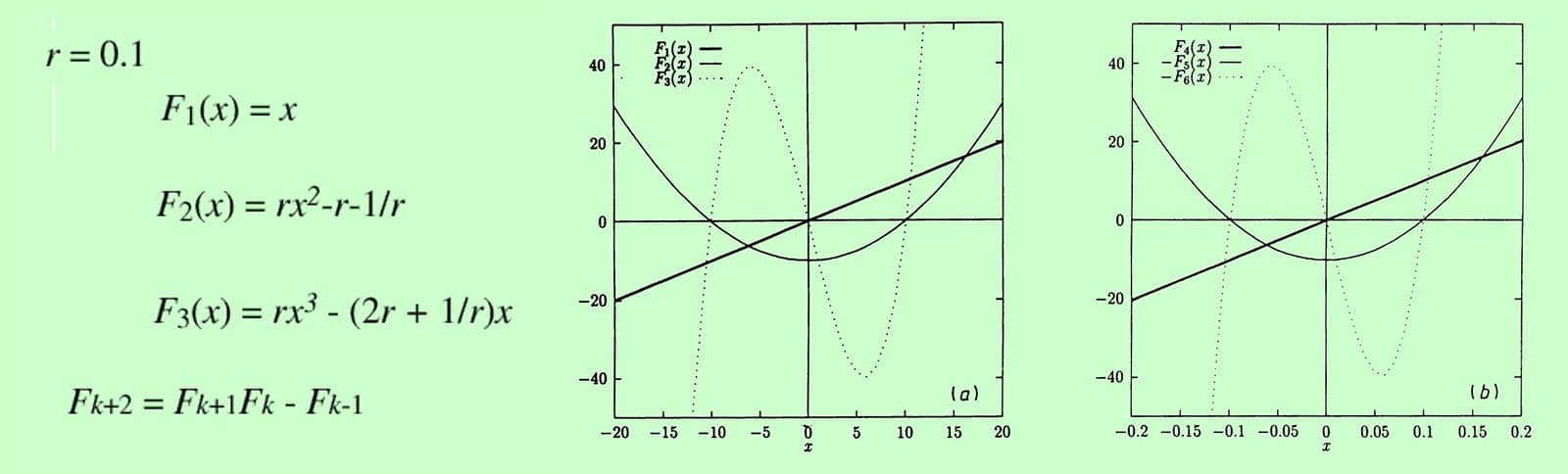
We present new polynomials with self-similar properties, which are obtained from the Fibonacci-chain model. The crystalline analogs are the Chebyshev polynomials of the first kind. The polynomials are akin to the fixed points of a renormalization-group equation. The structure of the zeros of the polynomials forms a tree, which we call the Fibonacci tree. Using this tree, we discuss the electronic spectrum of tight-binding models.